draw a plane in 3d

Pattern technique

Classification of some 3D projections

A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a ii-dimensional (second) surface. These projections rely on visual perspective and aspect analysis to projection a complex object for viewing capability on a simpler aeroplane. This concept of extending 2nd geometry to 3D was mastered by Heron of Alexandria in the first century.^[one] Heron could be called the father of 3D. 3D Projection is the basis of the concept for Computer Graphics simulating fluid flows to imitate realistic effects.^[two] Lucas Films 'ILM group is credited with introducing the concept (and even the term "Particle event").

In 1982, the first all-digital computer generated sequence for a picture show file was in: Star Trek II: The Wrath of Khan. A 1984 patent related to this concept was written by William E Masters, "Computer automated manufacturing procedure and organisation" US4665492A using mass particles to fabricate a loving cup.^[3] The process of particle degradation is 1 technology of 3D press.

3D projections use the principal qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret that the effigy or image as not actually flat (2d), just rather, as a solid object (3D) being viewed on a 2D display.

3D objects are largely displayed on ii-dimensional mediums (i.due east. paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using diverse geometric and optical techniques.

Overview [edit]

Several types of graphical projection compared

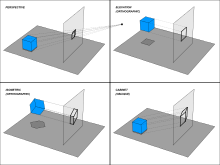
Various projections and how they are produced

Projection is achieved past the use of imaginary "projectors"; the projected, mental epitome becomes the technician's vision of the desired, finished picture.^{[ further explanation needed ]} Methods provide a uniform imaging process amid people trained in technical graphics (mechanical drawing, calculator aided blueprint, etc.). By following a method, the technician may produce the envisioned picture on a planar surface such equally drawing paper.

At that place are two graphical projection categories, each with its own method:

• parallel projection
• perspective projection

• 

• 

• 

• 

• 

• 

• 

Parallel project [edit]

Parallel projection corresponds to a perspective projection with a hypothetical viewpoint; i.e. i where the camera lies an infinite altitude abroad from the object and has an space focal length, or "zoom".

In parallel projection, the lines of sight from the object to the projection plane are parallel to each other. Thus, lines that are parallel in three-dimensional space remain parallel in the ii-dimensional projected prototype. Parallel projection as well corresponds to a perspective projection with an infinite focal length (the distance from a camera's lens and focal point), or "zoom".

Images drawn in parallel projection rely upon the technique of axonometry ("to measure forth axes"), as described in Pohlke's theorem. In general, the resulting image is oblique (the rays are non perpendicular to the image airplane); only in special cases the result is orthographic (the rays are perpendicular to the image aeroplane). Axonometry should not be confused with axonometric project, as in English literature the latter unremarkably refers only to a specific class of pictorials (meet below).

Orthographic projection [edit]

The orthographic projection is derived from the principles of descriptive geometry and is a two-dimensional representation of a three-dimensional object. Information technology is a parallel projection (the lines of projection are parallel both in reality and in the projection airplane). It is the projection type of pick for working drawings.

If the normal of the viewing plane (the camera direction) is parallel to one of the primary axes (which is the x, y, or z axis), the mathematical transformation is every bit follows; To projection the 3D betoken ${\displaystyle a_{x}}$ , ${\displaystyle a_{y}}$ , ${\displaystyle a_{z}}$ onto the 2d point ${\displaystyle b_{10}}$ , ${\displaystyle b_{y}}$ using an orthographic project parallel to the y axis (where positive y represents forwards direction - profile view), the post-obit equations tin be used:

${\displaystyle b_{10}=s_{ten}a_{x}+c_{x}}$

${\displaystyle b_{y}=s_{z}a_{z}+c_{z}}$

where the vector southward is an arbitrary scale gene, and c is an capricious offset. These constants are optional, and can exist used to properly align the viewport. Using matrix multiplication, the equations get:

${\displaystyle {\brainstorm{bmatrix}b_{ten}\\b_{y}\end{bmatrix}}={\begin{bmatrix}s_{x}&0&0\\0&0&s_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}+{\begin{bmatrix}c_{ten}\\c_{z}\cease{bmatrix}}.}$

While orthographically projected images represent the three dimensional nature of the object projected, they do not represent the object equally information technology would be recorded photographically or perceived by a viewer observing information technology straight. In item, parallel lengths at all points in an orthographically projected image are of the same scale regardless of whether they are far away or well-nigh to the virtual viewer. Every bit a upshot, lengths are not foreshortened as they would exist in a perspective project.

Multiview projection [edit]

Symbols used to define whether a multiview projection is either 3rd Angle (right) or First Angle (left).

With multiview projections, up to six pictures (called primary views) of an object are produced, with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of ii schemes: showtime-bending or third-bending projection. In each, the appearances of views may be thought of every bit beingness projected onto planes that form a 6-sided box around the object. Although six unlike sides can be fatigued, normally iii views of a drawing give enough data to make a 3D object. These views are known every bit front view, summit view, and end view. The terms elevation, program and department are also used.

Oblique project [edit]

Potting bench drawn in cabinet projection with an bending of 45° and a ratio of 2/three

Stone curvation drawn in war machine perspective

In oblique projections the parallel projection rays are not perpendicular to the viewing aeroplane as with orthographic projection, but strike the project plane at an angle other than ninety degrees. In both orthographic and oblique projection, parallel lines in infinite announced parallel on the projected prototype. Because of its simplicity, oblique projection is used exclusively for pictorial purposes rather than for formal, working drawings. In an oblique pictorial drawing, the displayed angles among the axes besides as the foreshortening factors (scale) are arbitrary. The distortion created thereby is usually attenuated by aligning i aeroplane of the imaged object to be parallel with the aeroplane of projection thereby creating a true shape, full-size paradigm of the chosen plane. Special types of oblique projections are:

Cavalier projection (45°) [edit]

In cavalier projection (sometimes cavalier perspective or loftier view indicate) a betoken of the object is represented past 3 coordinates, x, y and z. On the drawing, it is represented by only two coordinates, 10″ and y″. On the flat drawing, two axes, x and z on the figure, are perpendicular and the length on these axes are drawn with a one:1 scale; information technology is thus similar to the dimetric projections, although it is not an axonometric projection, as the third axis, here y, is drawn in diagonal, making an arbitrary angle with the ten″ centrality, usually xxx or 45°. The length of the third axis is not scaled.

Cabinet projection [edit]

The term cabinet projection (sometimes chiffonier perspective) stems from its use in illustrations by the furniture industry.^{[ commendation needed ]} Like cavalier perspective, one face of the projected object is parallel to the viewing airplane, and the third axis is projected equally going off in an angle (typically thirty° or 45° or arctan(ii) = 63.iv°). Unlike cavalier projection, where the third centrality keeps its length, with chiffonier projection the length of the receding lines is cut in half.

Military projection [edit]

A variant of oblique projection is called military project. In this case, the horizontal sections are isometrically drawn so that the floor plans are not distorted and the verticals are fatigued at an bending. The military projection is given by rotation in the xy-airplane and a vertical translation an corporeality z.^[4]

Axonometric project [edit]

Axonometric projections show an image of an object equally viewed from a skew direction in order to reveal all 3 directions (axes) of space in one picture.^[5] Axonometric projections may be either orthographic or oblique. Axonometric instrument drawings are often used to gauge graphical perspective projections, but at that place is attendant distortion in the approximation. Because pictorial projections innately comprise this distortion, in musical instrument drawings of pictorials slap-up liberties may and so be taken for economy of effort and all-time effect.^{[ clarification needed ]}

Axonometric projection is further subdivided into three categories: isometric projection, dimetric project, and trimetric projection, depending on the verbal angle at which the view deviates from the orthogonal.^{[6] [7]} A typical characteristic of orthographic pictorials is that 1 axis of infinite is usually displayed as vertical.

Axonometric projections are also sometimes known every bit auxiliary views, as opposed to the main views of multiview projections.

Isometric project [edit]

In isometric pictorials (for methods, see Isometric projection), the direction of viewing is such that the three axes of infinite appear equally foreshortened, and in that location is a common bending of 120° between them. The distortion caused by foreshortening is compatible, therefore the proportionality of all sides and lengths are preserved, and the axes share a common scale. This enables measurements to be read or taken directly from the drawing.

Dimetric projection [edit]

In dimetric pictorials (for methods, encounter Dimetric projection), the direction of viewing is such that two of the three axes of infinite announced as foreshortened, of which the attendant scale and angles of presentation are determined co-ordinate to the angle of viewing; the calibration of the third direction (vertical) is adamant separately. Approximations are common in dimetric drawings.

Trimetric project [edit]

In trimetric pictorials (for methods, see Trimetric project), the direction of viewing is such that all of the 3 axes of space appear unequally foreshortened. The scale forth each of the three axes and the angles among them are adamant separately as dictated by the angle of viewing. Approximations in Trimetric drawings are common.

Limitations of parallel projection [edit]

An case of the limitations of isometric projection. The top difference between the ruddy and blue assurance cannot be adamant locally.

The Penrose stairs depicts a staircase which seems to ascend (anticlockwise) or descend (clockwise) yet forms a continuous loop.

Objects drawn with parallel projection exercise non appear larger or smaller every bit they extend closer to or away from the viewer. While advantageous for architectural drawings, where measurements must exist taken directly from the image, the upshot is a perceived distortion, since unlike perspective project, this is not how our eyes or photography normally work. It also can hands result in situations where depth and altitude are difficult to gauge, as is shown in the illustration to the correct.

In this isometric drawing, the blue sphere is ii units higher than the scarlet 1. Nevertheless, this difference in tiptop is not apparent if one covers the right one-half of the picture, as the boxes (which serve every bit clues suggesting height) are then obscured.

This visual ambivalence has been exploited in op art, besides as "impossible object" drawings. M. C. Escher's Waterfall (1961), while not strictly utilizing parallel project, is a well-known example, in which a aqueduct of water seems to travel unaided along a downwardly path, only to then paradoxically fall in one case once more equally information technology returns to its source. The h2o thus appears to disobey the law of conservation of energy. An extreme instance is depicted in the movie Inception, where past a forced perspective trick an immobile stairway changes its connectivity. The video game Fez uses tricks of perspective to determine where a thespian tin can and cannot movement in a puzzle-similar fashion.

Perspective projection [edit]

Perspective of a geometric solid using two vanishing points. In this case, the map of the solid (orthogonal projection) is drawn beneath the perspective, as if angle the footing plane.

Axonometric projection of a scheme displaying the relevant elements of a vertical moving-picture show plane perspective. The standing point (P.S.) is located on the footing plane π, and the point of view (P.V.) is right to a higher place it. P.P. is its project on the picture aeroplane α. L.O. and L.T. are the horizon and the ground lines (linea d'orizzonte and linea di terra). The bold lines s and q lie on π, and intercept α at Ts and Tq respectively. The parallel lines through P.V. (in red) intercept L.O. in the vanishing points Fs and Fq: thus one tin draw the projections s′ and q′, and hence likewise their intersection R′ on R.

Perspective project or perspective transformation is a linear projection where three dimensional objects are projected on a film plane. This has the issue that distant objects appear smaller than nearer objects.

It as well ways that lines which are parallel in nature (that is, come across at the point at infinity) appear to intersect in the projected paradigm, for example if railways are pictured with perspective project, they announced to converge towards a single point, chosen the vanishing point. Photographic lenses and the human being middle work in the aforementioned style, therefore perspective projection looks near realistic.^[8] Perspective projection is unremarkably categorized into 1-bespeak, two-signal and iii-betoken perspective, depending on the orientation of the project plane towards the axes of the depicted object.^[9]

Graphical projection methods rely on the duality between lines and points, whereby 2 directly lines determine a point while 2 points make up one's mind a straight line. The orthogonal projection of the eye point onto the picture plane is called the principal vanishing point (P.P. in the scheme on the left, from the Italian term punto principale, coined during the renaissance).^[10]

Two relevant points of a line are:

• its intersection with the picture show aeroplane, and
• its vanishing signal, found at the intersection between the parallel line from the eye point and the flick plane.

The master vanishing signal is the vanishing point of all horizontal lines perpendicular to the moving picture plane. The vanishing points of all horizontal lines lie on the horizon line. If, as is often the case, the picture plane is vertical, all vertical lines are drawn vertically, and have no finite vanishing point on the picture plane. Various graphical methods can be easily envisaged for projecting geometrical scenes. For instance, lines traced from the eye point at 45° to the movie plane intersect the latter along a circumvolve whose radius is the distance of the center bespeak from the plane, thus tracing that circle aids the construction of all the vanishing points of 45° lines; in particular, the intersection of that circumvolve with the horizon line consists of two distance points. They are useful for drawing chessboard floors which, in turn, serve for locating the base of objects on the scene. In the perspective of a geometric solid on the right, after choosing the primary vanishing point —which determines the horizon line— the 45° vanishing bespeak on the left side of the drawing completes the characterization of the (equally distant) point of view. Two lines are drawn from the orthogonal projection of each vertex, i at 45° and one at xc° to the picture aeroplane. Afterwards intersecting the ground line, those lines become toward the distance point (for 45°) or the chief point (for 90°). Their new intersection locates the project of the map. Natural heights are measured above the ground line and then projected in the same way until they run into the vertical from the map.

While orthographic projection ignores perspective to let authentic measurements, perspective projection shows distant objects as smaller to provide additional realism.

Mathematical formula [edit]

The perspective projection requires a more involved definition as compared to orthographic projections. A conceptual assist to understanding the mechanics of this projection is to imagine the 2d projection as though the object(s) are being viewed through a camera viewfinder. The camera's position, orientation, and field of view command the beliefs of the projection transformation. The following variables are divers to describe this transformation:

• ${\displaystyle \mathbf {a} _{10,y,z}}$ – the 3D position of a indicate A that is to be projected.
• ${\displaystyle \mathbf {c} _{x,y,z}}$ – the 3D position of a point C representing the camera.
• ${\displaystyle \mathbf {\theta } _{x,y,z}}$ – The orientation of the camera (represented by Tait–Bryan angles).
• ${\displaystyle \mathbf {east} _{x,y,z}}$ – the display surface's position relative to the photographic camera pinhole C.^[xi]

Virtually conventions utilize positive z values (the plane being in front end of the pinhole), still negative z values are physically more than right, but the image volition be inverted both horizontally and vertically. Which results in:

When ${\displaystyle \mathbf {c} _{10,y,z}=\langle 0,0,0\rangle ,}$ and ${\displaystyle \mathbf {\theta } _{x,y,z}=\langle 0,0,0\rangle ,}$ the 3D vector ${\displaystyle \langle i,2,0\rangle }$ is projected to the 2D vector ${\displaystyle \langle 1,2\rangle }$ .

Otherwise, to compute ${\displaystyle \mathbf {b} _{10,y}}$ we first define a vector ${\displaystyle \mathbf {d} _{10,y,z}}$ equally the position of bespeak A with respect to a coordinate arrangement defined by the camera, with origin in C and rotated past ${\displaystyle \mathbf {\theta } }$ with respect to the initial coordinate arrangement. This is achieved by subtracting ${\displaystyle \mathbf {c} }$ from ${\displaystyle \mathbf {a} }$ and then applying a rotation by ${\displaystyle -\mathbf {\theta } }$ to the result. This transformation is oft called a camera transform , and can be expressed as follows, expressing the rotation in terms of rotations well-nigh the x, y, and z axes (these calculations presume that the axes are ordered as a left-handed organization of axes): ^{[12] [xiii]}

${\displaystyle {\brainstorm{bmatrix}\mathbf {d} _{x}\\\mathbf {d} _{y}\\\mathbf {d} _{z}\end{bmatrix}}={\brainstorm{bmatrix}1&0&0\\0&\cos(\mathbf {\theta } _{x})&\sin(\mathbf {\theta } _{x})\\0&-\sin(\mathbf {\theta } _{x})&\cos(\mathbf {\theta } _{x})\end{bmatrix}}{\brainstorm{bmatrix}\cos(\mathbf {\theta } _{y})&0&-\sin(\mathbf {\theta } _{y})\\0&1&0\\\sin(\mathbf {\theta } _{y})&0&\cos(\mathbf {\theta } _{y})\cease{bmatrix}}{\brainstorm{bmatrix}\cos(\mathbf {\theta } _{z})&\sin(\mathbf {\theta } _{z})&0\\-\sin(\mathbf {\theta } _{z})&\cos(\mathbf {\theta } _{z})&0\\0&0&one\end{bmatrix}}\left({{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\cease{bmatrix}}-{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}}\correct)}$

This representation corresponds to rotating by three Euler angles (more properly, Tait–Bryan angles), using the xyz convention, which can exist interpreted either as "rotate about the extrinsic axes (axes of the scene) in the club z, y, 10 (reading correct-to-left)" or "rotate nearly the intrinsic axes (axes of the photographic camera) in the guild ten, y, z (reading left-to-correct)". Annotation that if the camera is not rotated ( ${\displaystyle \mathbf {\theta } _{10,y,z}=\langle 0,0,0\rangle }$ ), then the matrices driblet out (as identities), and this reduces to simply a shift: ${\displaystyle \mathbf {d} =\mathbf {a} -\mathbf {c} .}$

Alternatively, without using matrices (let us replace ${\displaystyle a_{ten}-c_{ten}}$ with ${\displaystyle \mathbf {ten} }$ and and so on, and abbreviate ${\displaystyle \cos \left(\theta _{\alpha }\right)}$ to ${\displaystyle c_{\alpha }}$ and ${\displaystyle \sin \left(\theta _{\blastoff }\right)}$ to ${\displaystyle s_{\alpha }}$ ):

${\displaystyle {\begin{aligned}\mathbf {d} _{x}&=c_{y}(s_{z}\mathbf {y} +c_{z}\mathbf {ten} )-s_{y}\mathbf {z} \\\mathbf {d} _{y}&=s_{x}(c_{y}\mathbf {z} +s_{y}(s_{z}\mathbf {y} +c_{z}\mathbf {x} ))+c_{x}(c_{z}\mathbf {y} -s_{z}\mathbf {x} )\\\mathbf {d} _{z}&=c_{x}(c_{y}\mathbf {z} +s_{y}(s_{z}\mathbf {y} +c_{z}\mathbf {x} ))-s_{x}(c_{z}\mathbf {y} -s_{z}\mathbf {x} )\terminate{aligned}}}$

This transformed betoken can then be projected onto the 2D airplane using the formula (hither, x/y is used every bit the project airplane; literature also may use x/z):^[14]

${\displaystyle {\brainstorm{aligned}\mathbf {b} _{ten}&={\frac {\mathbf {e} _{z}}{\mathbf {d} _{z}}}\mathbf {d} _{x}+\mathbf {due east} _{x},\\[5pt]\mathbf {b} _{y}&={\frac {\mathbf {e} _{z}}{\mathbf {d} _{z}}}\mathbf {d} _{y}+\mathbf {e} _{y}.\terminate{aligned}}}$

Or, in matrix form using homogeneous coordinates, the system

${\displaystyle {\begin{bmatrix}\mathbf {f} _{x}\\\mathbf {f} _{y}\\\mathbf {f} _{west}\end{bmatrix}}={\begin{bmatrix}i&0&{\frac {\mathbf {due east} _{x}}{\mathbf {eastward} _{z}}}\\0&1&{\frac {\mathbf {e} _{y}}{\mathbf {e} _{z}}}\\0&0&{\frac {1}{\mathbf {e} _{z}}}\stop{bmatrix}}{\begin{bmatrix}\mathbf {d} _{x}\\\mathbf {d} _{y}\\\mathbf {d} _{z}\terminate{bmatrix}}}$

in conjunction with an argument using similar triangles, leads to division past the homogeneous coordinate, giving

${\displaystyle {\begin{aligned}\mathbf {b} _{x}&=\mathbf {f} _{x}/\mathbf {f} _{west}\\\mathbf {b} _{y}&=\mathbf {f} _{y}/\mathbf {f} _{westward}\cease{aligned}}}$

The altitude of the viewer from the display surface, ${\displaystyle \mathbf {e} _{z}}$ , directly relates to the field of view, where ${\displaystyle \blastoff =ii\cdot \arctan(ane/\mathbf {e} _{z})}$ is the viewed angle. (Note: This assumes that you map the points (-one,-i) and (1,1) to the corners of your viewing surface)

The higher up equations can as well be rewritten equally:

${\displaystyle {\begin{aligned}\mathbf {b} _{ten}&=(\mathbf {d} _{ten}\mathbf {south} _{x})/(\mathbf {d} _{z}\mathbf {r} _{x})\mathbf {r} _{z},\\\mathbf {b} _{y}&=(\mathbf {d} _{y}\mathbf {s} _{y})/(\mathbf {d} _{z}\mathbf {r} _{y})\mathbf {r} _{z}.\stop{aligned}}}$

In which ${\displaystyle \mathbf {due south} _{10,y}}$ is the display size, ${\displaystyle \mathbf {r} _{ten,y}}$ is the recording surface size (CCD or moving-picture show), ${\displaystyle \mathbf {r} _{z}}$ is the distance from the recording surface to the entrance pupil (camera center), and ${\displaystyle \mathbf {d} _{z}}$ is the distance, from the 3D betoken being projected, to the entrance pupil.

Subsequent clipping and scaling operations may exist necessary to map the 2d plane onto any item brandish media.

Weak perspective projection [edit]

A "weak" perspective projection uses the same principles of an orthographic project, but requires the scaling factor to be specified, thus ensuring that closer objects appear bigger in the projection, and vice versa. It tin can exist seen as a hybrid between an orthographic and a perspective projection, and described either as a perspective projection with individual indicate depths ${\displaystyle Z_{i}}$ replaced past an average constant depth ${\displaystyle Z_{\text{ave}}}$ ,^[xv] or simply as an orthographic projection plus a scaling.^[16]

The weak-perspective model thus approximates perspective project while using a simpler model, similar to the pure (unscaled) orthographic perspective. It is a reasonable approximation when the depth of the object along the line of sight is small compared to the altitude from the camera, and the field of view is small. With these conditions, it can be causeless that all points on a 3D object are at the same distance ${\displaystyle Z_{\text{ave}}}$ from the camera without significant errors in the projection (compared to the total perspective model).

Equation

${\displaystyle {\begin{aligned}&P_{x}={\frac {10}{Z_{\text{ave}}}}\\[5pt]&P_{y}={\frac {Y}{Z_{\text{ave}}}}\terminate{aligned}}}$

assuming focal length $f=1$ .

Diagram [edit]

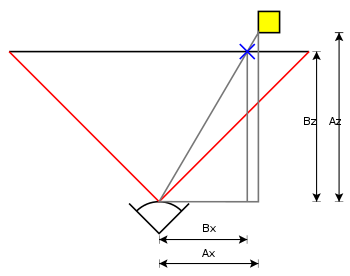
To determine which screen 10-coordinate corresponds to a point at ${\displaystyle A_{x},A_{z}}$ multiply the point coordinates by:

${\displaystyle B_{10}=A_{x}{\frac {B_{z}}{A_{z}}}}$

where

${\displaystyle B_{ten}}$ is the screen ten coordinate

${\displaystyle A_{x}}$ is the model x coordinate

${\displaystyle B_{z}}$ is the focal length—the axial distance from the photographic camera center to the image aeroplane

${\displaystyle A_{z}}$ is the subject distance.

Because the camera is in 3D, the same works for the screen y-coordinate, substituting y for x in the above diagram and equation.

You can employ that to do clipping techniques, replacing the variables with values of the point that'due south are out of the FOV-angle and the point inside Camera Matrix.

This technique, also known as "Inverse Photographic camera", is a Perspective Project Calculus with known values to summate the terminal point on visible angle, projecting from the invisible bespeak, after all needed transformations finished.

Run into also [edit]

• 3D computer graphics
• Camera matrix
• Reckoner graphics
• Cantankerous section (geometry)
• Cantankerous-sectional view
• Curvilinear perspective
• Cutaway drawing
• Descriptive geometry
• Engineering cartoon
• Exploded-view drawing
• Homogeneous coordinates
• Homography
• Map projection (including Cylindrical projection)
• Multiview projection
• Perspective (graphical)
• Plan (cartoon)
• Technical drawing
• Texture mapping
• Transform, clipping, and lighting
• Video bill of fare
• Viewing frustum
• Virtual globe

References [edit]

1. ^ Peddie, Jon. (2013). The history of visual magic in computers : how beautiful images are made in CAD, 3D, VR and AR. London: Springer. p. 25. ISBN978-i-4471-4932-3. OCLC 849634980.
2. ^ Peddie, Jon. (2013). The history of visual magic in computers : how beautiful images are made in CAD, 3D, VR and AR. London: Springer. pp. 67–69. ISBN978-i-4471-4932-3. OCLC 849634980.
3. ^ Patent 4665492, Effigy 2A, 2B and 2C.
4. ^ "Axonometric projections - a technical overview". Retrieved 24 April 2015.
5. ^ Mitchell, William; Malcolm McCullough (1994). Digital pattern media. John Wiley and Sons. p. 169. ISBN978-0-471-28666-0.
6. ^ Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell Academy Printing. p. 22. ISBN978-0-8014-7280-0.
7. ^ McReynolds, Tom; David Blythe (2005). Avant-garde graphics programming using openGL. Elsevier. p. 502. ISBN978-1-55860-659-3.
8. ^ D. Hearn, & M. Baker (1997). Calculator Graphics, C Version. Englewood Cliffs: Prentice Hall], affiliate 9
9. ^ James Foley (1997). Reckoner Graphics. Boston: Addison-Wesley. ISBN 0-201-84840-six], affiliate 6
10. ^ Kirsti Andersen (2007), The geometry of an art, Springer, p. xxix, ISBN9780387259611
11. ^ Ingrid Carlbom, Joseph Paciorek (1978). "Planar Geometric Projections and Viewing Transformations" (PDF). ACM Computing Surveys. 10 (4): 465–502. CiteSeerX10.1.ane.532.4774. doi:10.1145/356744.356750. S2CID 708008.
12. ^ Riley, K F (2006). Mathematical Methods for Physics and Engineering . Cambridge University Press. pp. 931, 942. doi:10.2277/0521679710. ISBN978-0-521-67971-eight.
13. ^ Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). Reading, Mass.: Addison-Wesley Pub. Co. pp. 146–148. ISBN978-0-201-02918-5.
14. ^ Sonka, One thousand; Hlavac, Five; Boyle, R (1995). Paradigm Processing, Analysis & Machine Vision (2d ed.). Chapman and Hall. p. xiv. ISBN978-0-412-45570-4.
15. ^ Subhashis Banerjee (2002-02-18). "The Weak-Perspective Camera".
16. ^ Alter, T. D. (July 1992). 3D Pose from three Corresponding Points under Weak-Perspective Projection (PDF) (Technical report). MIT AI Lab.

Further reading [edit]

• Kenneth C. Finney (2004). 3D Game Programming All in One . Thomson Course. p. 93. ISBN978-1-59200-136-ane. 3D projection.
• Koehler; Dr. Ralph (December 2000). 2D/3D Graphics and Splines with Source Code. ISBN978-0759611870.

External links [edit]

• Creating 3D Environments from Digital Photographs

burksblipts.blogspot.com

Source: https://en.wikipedia.org/wiki/3D_projection

Share this post